円周率は何桁まで覚えておくとよいのか

昭和60年代前半，当時小学生だったタロウ少年は，円周率を17桁，3.1415926535897932まで覚えました．覚える桁数はそれでよかったのか，という話です．

拙著『コンピュータでとく数学』について，こんな質問がありました．

p.29に倍精度でのπの近似値は 884279719003555/281474976710656 とありますが，245850922/78256779 でよいのではないでしょうか．

良い質問です．というか，そんなに丁寧に読んでもらえるとは思わなかったというのが正直なところです．

因みに，分子の245850922は，Numerators of convergents to Piのa(16)ですね．

短い回答

次の二種類の近似があるせいで，わかりにくいのでしょう．

数を浮動小数点数で近似すること
πを有理数で近似すること

『コンピュータでとく数学』で重要なのは1です．数xを浮動小数点数で表すときの，式(2.10)の意味での厳密値をf(x)とします．

A:=884279719003555/281474976710656
B:=245850922/78256779

とすると
f(A)=f(B)=f(π)=A≠B
です．つまり，A, B, πは浮動小数点数にすると全て同じ値になりますが，その値と等しいのはAだということです．

上記の2「πを有理数で近似すること」についての話は長くなります．『コンピュータでとく数学』とはほとんど関係のない話です．

長い回答（話）

πを有理数で近似する場合に，最もよく使われるのは3.14 (=314/100)でしょう．3.1415 (=31415/10000)くらいまでなら，覚えている人は多いかも知れません．

もっと覚えるなら，3.1415926535897932（17桁）がお勧めです．

理由1：浮動小数点数（IEEE 754のbinary64）で表現できる円周率の「最良」，つまりπとの差の絶対値が最小の近似値は884279719003555/281474976710656（約3.14159265358979312）です．正しいのは16桁までですが，次のA, B, Cのうちで最良の近似値に最も近いのはB（17桁）です．

A:=3.141592653589793（16桁）
B:=3.1415926535897932（17桁）
C:=3.14159265358979323（18桁）

理由2：10進小数での入力3.1415926535897932（17桁）がπのbinary64での最良の近似値になります．1桁少ない3.141592653589793（16桁）も最良の近似値になりますが，理由1があるため3.1415926535897932がよいでしょう．

近似に使う有理数の分母は，10のベキ乗の場合に限りません．例えば，22/7 （約3.142）は314/100より簡潔で正確です．355/113（約3.1415929）も覚えやすくてよいです．

昭和の時代に近所の図書館で借りて読んだ，木村良夫『パソコンで遊ぶ数学: BASICの基礎からグラフィックスまで』（ブルーバックス, 1986）（以下，木村本）に，πを有理数で近似する，次のようなプログラムが載っていました¹．

100 REM ***** Fraction.1986.8.29
105  DEFDBL A-Z
110  A=4*ATN(1)
120  N=1:D=1
130  L=A*N
140  M=INT(L)
150  IF M+1-L<L-M THEN M=M+1
160  E=ABS(A-M/N)
170  IF E>=D GOTO 200
180  PRINT M;"/";N,M/N
185  IF E=0 THEN END
190  D=E
200  N=N+1
210  GOTO 130

問題を整理しましょう．MとNを整数とします．

問題P1：πを，M/Nで近似する．
問題P2：πを近似する浮動小数点数Aを，浮動小数点数M/Nで近似する．

ここで解こうとしているのは問題P2です．昭和のパソコンでは，Aに近づけるのが大変でしたが，現代では，（倍精度なら）Aとの差を0にできてしまうので，Aが本当にπの最良の近似値になっているかが重要になります．

P1とP2は同じ問題のように見えます．実際，後で示すIEEE 754での解とMBFでのP2の解はP1の解と同じです．しかし，BCDでのP2の解はP1の解と異なります．P2の解としては，5419351/1725033=3.1415926535897よりも，10838702/3450066=3.1415926535898が（πに近くて）良いのですが，P1の解としては，10838702/3450066よりも，これを約分した5419351/1725033が（単純で）良いのです．

結果の概要

いくつかのシステムで試した結果を表にまとめます．規格による精度の違いが結果に表れています．

時代	システム	規格	最終結果	10進小数表示
昭和	MSX-BASIC	BCD	`10838702/3450066`	約3.14159265358981
現代	C言語	IEEE 754	`245850922/78256779`	約3.14159265358979316
現代	C言語	x87の80ビット拡張形式	`8717442233/2774848045`	約3.1415926535897932385
現代	bwBASIC	IEEE 754	`245850922/78256779`	約3.14159265358979316
昭和	N-BASIC	MBF	`657408909/209259755`	約3.14159265358979322
現代	PC-BASIC	MBF	`657408909/209259755`	約3.14159265358979322

（昭和）PC-8001 N-BASIC

お前の前にいるのは，四十年以上生きたプログラマだ．

家にあったマイコン（PC-8001，N-BASIC）での計算を，実機の32倍速で動くというPC-8001のエミュレータで再現します（コードを入力してRUNで実行．STOPキーで停止）．

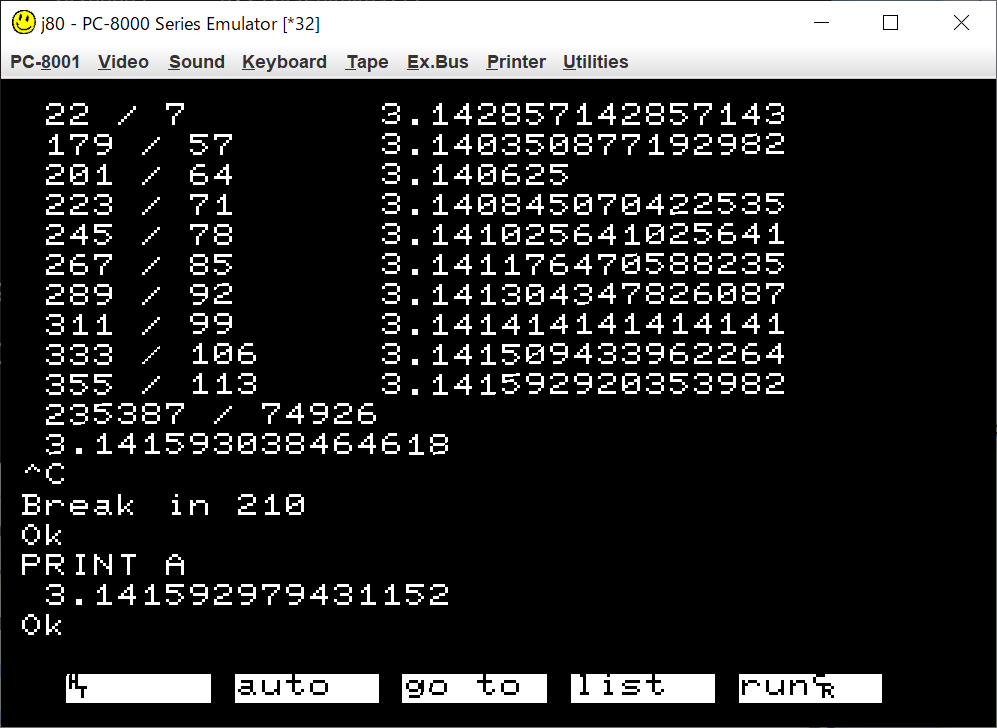
PC-8001で実行している様子

PC-8001のVirtual Keyboard

失敗1（`ATN`は単精度）

355/113の次が235387/74926になっているのは，木村本に書かれているとおり，誤りです．誤りの原因は，ATNが単精度であることです．110 A=4*ATN(1)で得るπの近似値が倍精度では不正確（約3.1415929）なので，計算を進める意味がありません．

失敗2（πの10進小数表示）

とりあえず，覚えていた17桁を使って110 A=3.1415926535897932として計算します．実機を何日も動かしていたら，プログラムは742972117 / 236495370 3.141592653589793を出力して停止したはずです．

ここに罠があります．

N-BASICの浮動小数点数はMicrosoft Binary Format (MBF)です．A=3.1415926535897932は，MBFの倍精度で表現できるπの最良の近似値ではありません．バイト列（リトルエンディアン）を比べると次のようになります（1バイト目が違います）．

C4 68 21 A2 DA 0F 49 82（A=3.1415926535897932）．
C2 68 21 A2 DA 0F 49 82（πの最良の近似値．補足1を参照）

ですから，A=3.1415926535897932を使うのは誤りなのですが，PRINT Aの結果は3.141592653589793なので，小学生はこの罠に気付かないでしょう．

因みに，Aの1バイト目はPRINT HEX$(PEEK(VARPTR(A)))で確認できます²．

成功

Aの1バイト目をC2に書き換えます．

110  A=3.1415926535897932:POKE VARPTR(A),&HC2

2GHzで動くというM88 emulatorで試すと，プログラムは657408909 / 209259755 3.141592653589793を出力して停止します（πの最良の近似値との差は0）．

罠の一覧

バイト列が?? 68 21 A2 DA 0F 49 82（??はB4からC7）になる20個の数は全て，PRINTで表示させた結果は3.141592653589793で，それでは区別できません．

10 DEFDBL A
20 A=3.141592653589793#
30 FOR B=&HB3 TO &HC8
40   POKE VARPTR(A),B:PRINT A;
50 NEXT B

πのMBFでの近似値の1バイト目を表にまとめます（マチンの公式については補足2を参照）．

1バイト目	入力方法
`C2`（最良）	`A=3.1415926535897932:POKE VARPTR(A),&HC2`
`C2`（最良）	N88-BASICでマチンの公式（修正2, 3）
`C2`（最良）	PC-BASICで19桁入力
`C2`（最良）	PC-BASICでマチンの公式（修正1）
`C3`	N88-BASICでマチンの公式（修正3）
`C4`	N(88)-BASICで17桁入力
`C5`	N88-BASICでマチンの公式（修正2）
`C6`	N-BASICでマチンの公式（修正1, 2, 3）
`C6`	N88-BASICでマチンの公式（修正前）
`C7`	N-BASICでマチンの公式（修正1, 3）
`CB`	N-BASICでマチンの公式（修正1, 2）
`CC`	N-BASICでマチンの公式（修正1）

（昭和）MSX-BASIC

当時，少しでも先の結果を知りたいと思って，高性能なMSX2を持っていた友達に，プログラムを電話で読み上げて伝えて，実行してもらおうとしました（付き合ってくれる友達がすごいですね．何て頼んだんだろう）．プログラムが誤って伝わり，正しく実行できなかったのを，その友達のお父さんが直してくれて，結果をプリンタに出力してくれたことに驚愕しました．（インターネットのメールはなく，家庭用のプリンタも珍しかった時代です．）

子供には心の支えになる大人の存在が必要ですから．

実機の10倍速で動くというMSXのエミュレータで試します（コードは最初のまま．Ctrl-STOPで停止．参考：プログラムのロード方法）³．

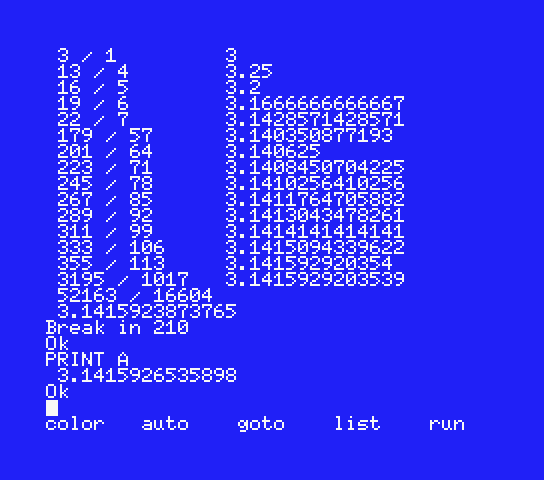
MSXで実行している様子

実機を動かし続けていたら，プログラムは10838702 / 3450066 3.1415926535898を出力して停止したはずです（πの最良の近似値との差は0）．

少年達は，N-BASICとMSX-BASICで結果が異なることに気付いたでしょうか．

結果が異なるのは，採用している浮動小数点数の規格が異なるからです．

N-BASICの浮動小数点数がMBFだったのに対して，MSX-BASICの浮動小数点数はBCDです．MSX-BASICの倍精度では，数の10進小数表示14桁を，各桁4ビット，全56ビットで表します．

この形式で表せる，πの最良の近似値は3.1415926535898です．4*ATN(1)はこれと等しいです．

N-BASICでは，PRINTの結果が3.141592653589793になる浮動小数点数が20個もありました．MSX-BASICにはそういうことはありません．性能はともかく，小学生にとってわかりやすかったのは間違いないです．

現代

Dockerで試します．

docker run --rm -it ubuntu
apt update
cd

（現代）C言語

C言語を試します．まずはdoubleの場合．

apt install -y gcc

cat << "EOF" > pi.c
#include <stdio.h>
#include <math.h>

int main() {
    double A, D, E, L, M, N;
    A = 4 * atan(1);
    N = 1, D = 1;
    while (1) {
        L = A * N;
        M = floor(L);
        if (M + 1 - L < L - M) M = M + 1;
        E = fabs(A - M / N);
        if (E < D) {
            printf("%.0f / %.0f\t %.17f\n", M, N, M / N);
            if (E == 0) break;
            D = E;
        }
        N = N + 1;
    }
    return 0;
}
EOF

gcc -O3 -Wall pi.c -lm && ./a.out

プログラムが245850922 / 78256779 3.14159265358979312を出力して停止するまでは一瞬です（πの最良の近似値との差は0）．

次にUbuntu x86_64上のGCCのlong double（x87の80ビット拡張形式）の場合．

cat << "EOF" > pi-longdouble.c
#include <stdio.h>
#include <math.h>

int main() {
    long double A, D, E, L, M, N;
    A = 4 * atanl(1);
    N = 1, D = 1;
    while (1) {
        L = A * N;
        M = floorl(L);
        if (M + 1 - L < L - M) M = M + 1;
        E = fabsl(A - M / N);
        if (E < D) {
            printf("%.0Lf / %.0Lf\t%.19Lf\n", M, N, M / N);
            if (E == 0) break;
            D = E;
        }
        N = N + 1;
    }
    return 0;
}
EOF

gcc -O3 -Wall pi-longdouble.c -lm && ./a.out

プログラムは8717442233 / 2774848045 3.1415926535897932385を出力して停止します（πの最良の近似値14488038916154245685/4611686018427387904との差は0）．

4倍精度（メモ）

cat << "EOF" > pi-quadmath.c
#include <stdio.h>
#include <quadmath.h>

int main() {
    char b1[128], b2[128], b3[128];
    __float128 A, D, E, L, M, N;
    A = 4 * atanq(1);
    N = 1, D = 1;
    while (1) {
        L = A * N;
        M = floorq(L);
        if (M + 1 - L < L - M) M = M + 1;
        E = fabsq(A - M / N);
        if (E < D) {
            quadmath_snprintf(b1, sizeof(b1), "%.0Qf", M);
            quadmath_snprintf(b2, sizeof(b2), "%.0Qf", N);
            quadmath_snprintf(b3, sizeof(b3), "%.37Qg", M / N);
            printf("%s / %s\t%s\n", b1, b2, b3);
            if (E == 0) break;
            D = E;
        }
        N = N + 1;
    }
    return 0;
}
EOF

gcc -O3 -Wall pi-quadmath.c -lquadmath && ./a.out

（現代）bwBASIC

bwBASICを試します．（180の正しい書き方がわかりません．）

apt install -y bwbasic

cat << "EOF" > bw.bas
REM ***** Fraction.1986.8.29
A=4*ATN(1)
N=1:D=1
L=A*N
M=INT(L)
IF M+1-L<L-M THEN M=M+1
E=ABS(A-M/N)
IF E>=D THEN GOTO 200
PRINT USING "# / #    #.###############";M;N;M/N
IF E=0 THEN END
D=E
N=N+1
GOTO 130
EOF

bwbasic bw.bas

しばらく待つと，プログラムは245850922 / 78256779 3.14159265358979312を出力して停止します（SYSTEMで終了．πの最良の近似値との差は0）．

（現代）PC-BASIC

PC-BASICを試します．高速化のために，PyPyを使います．

A=3.141592653589793238（19桁）とすると，Aの1バイト目がC2になります（POKEは使えないようです）．タロウ少年は，19桁まで覚えるべきだったかもしれません．

apt install -y git pypy3
git clone https://github.com/robhagemans/pcbasic.git

cat << "EOF" > pc.bas
REM ***** Fraction.1986.8.29
DEFDBL A-Z
A=3.141592653589793238
PRINT HEX$(PEEK(VARPTR(A)))
N=1:D=1
L=A*N
M=INT(L)
IF M+1-L<L-M THEN M=M+1
E=ABS(A-M/N)
IF E>=D GOTO 200
PRINT M;"/";N,M/N
IF E=0 THEN END
D=E
N=N+1
GOTO 130
EOF

pypy3 pcbasic/run-pcbasic.py -n pc.bas

しばらく待つと，プログラムは657408909 / 209259755 3.141592653589793を出力して停止します（SYSTEMで終了．πの最良の近似値との差は0）．

補足1：MBFの倍精度で表現できるπの最良の近似値

MBFの倍精度で表現できるπの最良の近似値は

s:=0₂
e:=10000010₂
f:=1001001000011111101101010100010001000010110100011000010₂

として，(-1)^s×(1+f×2^-55)×2^(e-129)=28296951008113761/9007199254740992（約3.141592653589793227）です．

「e, s, f」をまとめて16進数で表すと，82 49 0F DA A2 21 68 C2です．メモリ上ではC2 68 21 A2 DA 0F 49 82（リトルエンディアン）となります（1バイト目はC2）．

(* Mathematica *)
s = 0;
e = 2^^10000010;
f = 2^^1001001000011111101101010100010001000010110100011000010;
x = (-1)^s (1 + f 2^(-55)) 2^(e - 129)
N[x, 20]
BaseForm[2^56 e + 2^55 s + f, 16]

補足2：マチンの公式＋arctanのマクローリン展開

木村本では，4*ATN(1)でπの近似値を求めるのに失敗した後で，マチンの公式とarctanのマクローリン展開を使う方法が試されています．しかし，小学生に理解できたとは思えません．実行しても良い結果は得られなかったでしょう．

πの近似値を求める部分は次のとおりです⁴．

100 REM ***** FRACT2 1986.9.1
110  DEFDBL A,D,E,L,M,N,X,Y,Z
120  K=11
130  X=1/5#
140  GOSUB 200
150  Z=Y
160  X=1/239#
170  GOSUB 200
180  A=16*Z-4*Y
190  GOTO 290
200 REM *** arctan
210  Y=0
220  FOR I=1 TO K
230    J=2*I-1
240    IF I MOD 2=0 GOTO 260
250    Y=Y+X^J/J:GOTO 270
260    Y=Y-X^J/J
270  NEXT I
280  RETURN
290 REM ***** Fraction
291  PRINT A
292  PRINT HEX$(PEEK(VARPTR(A)))

250と260で使うベキ乗「^」は，N-BASICでは単精度なので，このままではうまく行きません．

次のように修正して実行します．

ベキ乗をFOR文で計算します．
マクローリン展開の次数Kを12にします．（13以上にしても改善しません．）
マクローリン展開を，次数の高い方から計算します．

120  K=12
220  FOR I=K TO 1 STEP -1
231    DEFDBL P:P=1
232    FOR R=1 TO J
233      P=P*X
234    NEXT R
240    IF I MOD 2=0 GOTO 260
250    Y=Y+P/J:GOTO 270
260    Y=Y-P/J

PRINT Aの結果は3.141592653589793になりますが，Aの1バイト目はC6なので，これはπの最良の近似値ではありません（最良はC2）⁵．

蛇足

木村本は，私にとって初めての，エレガントな証明がわからない定理が載っていた，大事な本でもあります．（引用中の数は1以上9以下の整数のこと）

4つの数が0を含まず，しかもすべて互いに異なっているなら，この4つの数から四則で10をつくることができる．

この本を借りた図書館のOPACを調べると，残念なことに除籍になってしまったようなので，古書で入手しました．やはり，大事な本は買わなければなりません．

オリジナルではPRINTはLPRINT．木村本の通りに105 DEFDBL A-Zを補いました．また，πの近似値との差が0になったら終了するように，185を追加しました． ↩
Aのメモリ上での表現は，PRINT HEX$(VARPTR(A))の結果をXXXXとして，MONとしてマシン語モニタに入って，DXXXXとしても確認できます（Ctrl-Bで終了）．マシン語モニタでTMとした画面を約40年ぶりに見ました． ↩
WebMSX（ブラウザで動くエミュレータ）も便利です． ↩
オリジナルでは，130と160は10進小数表示でしたが，#を付けるなら分数で書いても大丈夫です．結果の確認用に，291と292を追加しました． ↩
N88-BASICのベキ乗「^」は倍精度なので，最初のコードのまま計算できますが，その結果のAの1バイト目はC6です．それを有理数で近似するプログラムは，914098533 / 290966600 3.141592653589793を出力して停止します．修正2（120 K=12），修正3（220 FOR I=K TO 1 STEP -1）を施すと，Aの1バイト目はC2になります（最良）． ↩