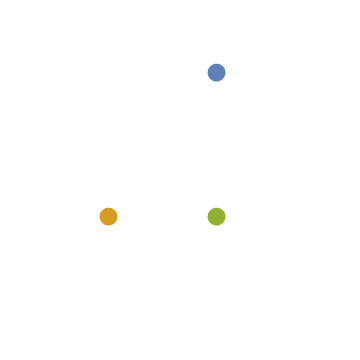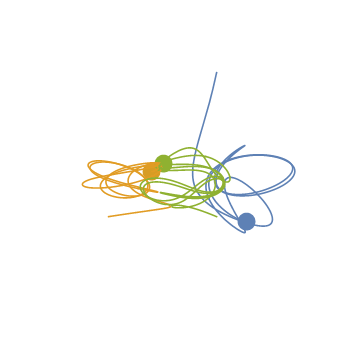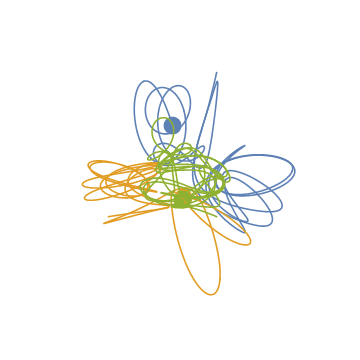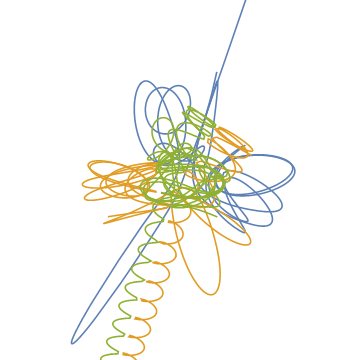三体問題を解く難しさ
三体問題の例として,ピラゴラス三体問題を試します。三体問題を解くのは難しいということを知っていると,小説『三体』をもっと楽しめるかもしれません。
ピラゴラス三体問題は,図のように,質量3, 4, 5の質点が,辺の長さが3, 4, 5の三角形の頂点で静止している状態の,その後の変化を調べる問題です。
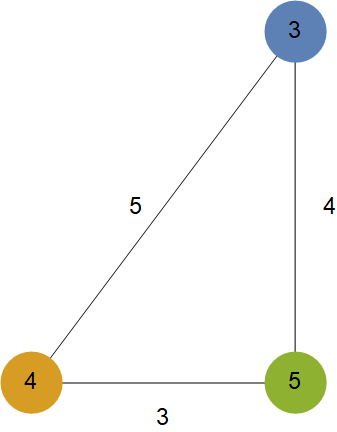
こういう状況をシミュレートするMathematicaの関数NBodySimulationを使います。
tmax = 70;
data = NBodySimulation["InverseSquare", {
<|"Mass" -> 3, "Position" -> { 1, 3}, "Velocity" -> {0, 0}|>,
<|"Mass" -> 4, "Position" -> {-2, -1}, "Velocity" -> {0, 0}|>,
<|"Mass" -> 5, "Position" -> { 1, -1}, "Velocity" -> {0, 0}|>},
tmax];
ParametricPlot[Evaluate[data[All, "Position", t]], {t, 0, tmax}]
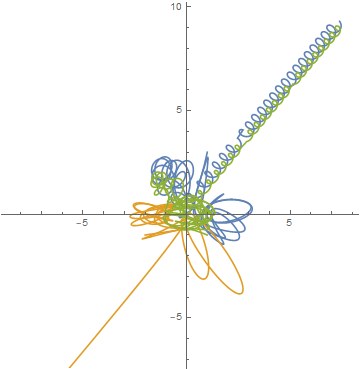
シミュレートできているように見えますが,(保存されるはずの)全エネルギーの時間変化を見ると,うまく行ってないことがわかります。
Plot[Evaluate[data["TotalEnergy", t]], {t, 0, tmax}]
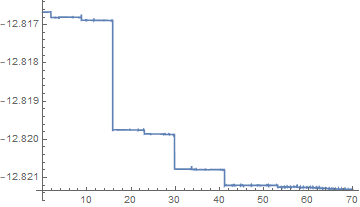
これは,data["HamiltonEquations"]として得られるの運動方程式をそのままNDSolveで解いた結果のようです。この問題では少なくとも,全エネルギー,運動量,角運動量が保存されなければならないのですが,NBodySimulationにそういう制約を入れる方法がよくわかりません。
三体問題を解くのは難しいです。