谷合廣紀(著),辻真吾(監修)『Pythonで理解する統計解析の基礎』
谷合廣紀(著),辻真吾(監修)『Pythonで理解する統計解析の基礎』(技術評論社,2018)は,統計学の勉強にPythonを活用することを提案する書籍です。「PYTHON × MATH SERIES」というシリーズの最初の1冊のようです。勉強に使う道具として紙と鉛筆を想定して書かれた教科書を読むのはなかなか大変なので,こうやってコンピュータを活用する教科書がどんどん出てくるといいと思います。
対象を統計に限定するなら(現時点では)PythonよりRが向いていると思いますし,実際,Rで統計を学ぶ教科書はたくさん出ていますが,統計以外も扱うシリーズを展開するならRより汎用的なPythonで,ということになるのでしょう。
Rubyを使ったシリーズになりそうでならなかった『プログラミングのための確率統計』も良書でしたが,『Pythonで理解する統計解析の基礎』はほとんどすべての事例にPythonでの確認作業が付いているという点で,コンピュータを活用するという方針が徹底しています。
(個人的には,統計限定でもシリーズでも,RやPython,RubyよりMathematicaがいいと思いますが,それはまた別の話。)
著者の谷合さんは,将棋の奨励会三段かつ東大大学院情報理工学研究科の院生だそうです。どちらもプロの一歩手前(?)とはいえ,こういう肩書を併せ持つというのはかなりすごいことです。
追記:著者の谷合廣紀さんは,2020年3月に4段昇段を決めました。
閑話休題。本書は,コンピュータ(Python)を活用することで効率よく統計を学ぶことを目指していて,その目標は達成されていると思います。Python自体やプログラミングを学ぶための本ではないので,そういうものを探している人は,他をあたった方がいいでしょう。
「SciPyで一発!」みたいなのが私の好みですが,そういう過激なことはせずに,定義どおりの計算をNumPyで地味にやってみせてから,実はSciPyなら一発という具合で説明されているので(例外あり),正統派(?)からも怒られないのではないかと思います。ただ,NumPyでの地味な計算とSciPyでのお手軽な計算が見分けにくいところがあるので,お手軽なところに気付かずに,「地味で大変だなあ」で終わってしまわないか心配です。(そういう人へ:よく読むと,正確で手軽な方法が後で出てきますよ。)
何というか,本書は将棋の指導対局のようで,著者(上手)はいろいろ読みを入れているにもかかわらず,それをぶちまけて学習者(下手)を溺れさせるようなことはせず,最も気持ちいい形で理解できるように配慮して書かれています。ただ,ちょっと親切すぎるというか,狙いすぎているところがあって,いざ読者が自分で試してみようと思ったときに,著者が見えないところで周到にしていた配慮に気付かずにハマってしまう,ということがあるかもしれません。(指導対局で理解したはずの手筋を実戦で試してうまく行かなかったからといって,指導対局が悪かったということにはなりません。)
例を挙げましょう。(読者が気にしなくてすむように著者が配慮したところをあえて蒸し返します。)
- xが出る確率密度がf(x)=2x (0 ≦ x ≦ 1)であるような,(整数でなく実数を出力する)ルーレットがあるとします。(p.126)
- ルーレットを2回まわして,出た数をA,Bとします。(p.138)
- X = A + B,Y = Aとします(A = Y,B = X - A = X - Y)。
- このとき,(X, Y)の確率密度f(x, y)は0 ≦ y ≦ 1かつ0 ≦ x - y ≦1のときは 4y(x - y),それ以外のときは0となります。
私にはSciPyすら大変なので,Mathematicaで確認します。
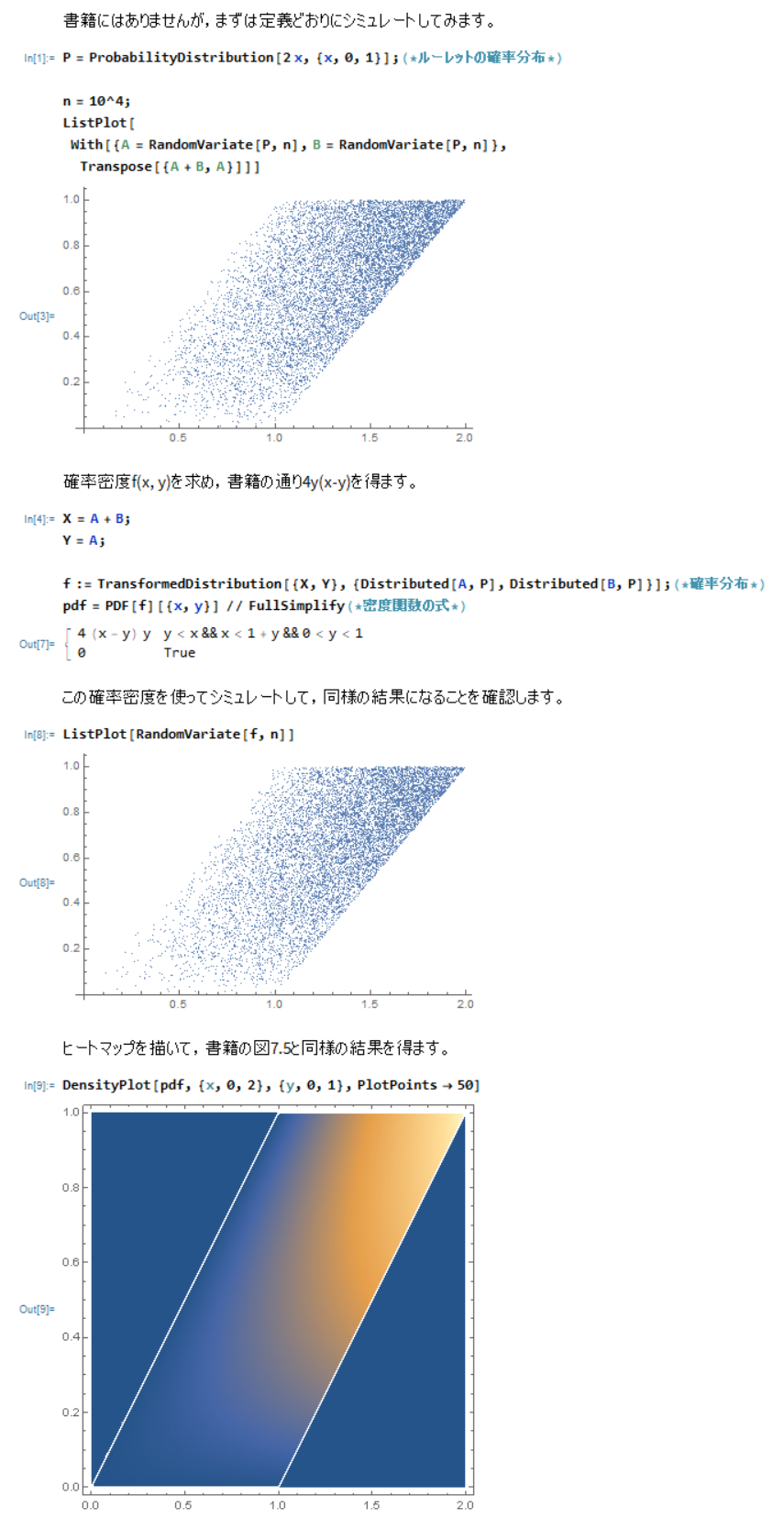
キャプチャ中のコードは以下の通りです。クラウド(こちらあるいはこちら)でも動きます。
P = ProbabilityDistribution[2 x, {x, 0, 1}];(*ルーレットの確率分布*)
n = 10^4;
ListPlot[
With[{A = RandomVariate[P, n], B = RandomVariate[P, n]},
Transpose[{A + B, A}]]]
X = A + B;
Y = A;
f := TransformedDistribution[{X, Y}, {Distributed[A, P], Distributed[B, P]}];(*確率分布*)
pdf = PDF[f][{x, y}] // FullSimplify(*密度関数の数式*)
ListPlot[RandomVariate[f, n]]
DensityPlot[pdf, {x, 0, 2}, {y, 0, 1}, PlotPoints -> 50]
周辺確率密度関数を求めます。「2変数関数のうち1変数のみで積分するといった関数は実装されていない(p.141)」Pythonでは面倒ですが,Mathematicaでは,式をそのまま書くだけです(ここで扱っている例なら解析的に計算できます。結果は割愛)
tmp = Integrate[pdf, {y, -Infinity, Infinity}];
Plot[tmp, {x, 0, 2}](*図7.6左*)
tmp = Integrate[pdf, {x, -Infinity, Infinity}];
Plot[tmp, {y, 0, 1}](*図7.6右*)
ここまでは問題なく進められるのですが,先の手順4を,次のように誤解されるのが心配です。
(X, Y)の確率密度f(x, y)は0 ≦ A = y ≦ 1かつ0 ≦ B = x - y ≦1のときは f(A)f(B) = f(y)f(x - y) = 4y(x - y),それ以外のときは0となります。(誤解)
こういう理解でX = A + B^2,Y = A (A = Y,B = sqrt(X - Y))の場合を試すと失敗します。f(x, y) = 4y(x - y)だと誤解しているからです。正しくは,∬f(A)f(B)dAdB = ∬f(y)f(sqrt(x - y)))|J|dxdyなのでf(x, y) = f(y)f(sqrt(x - y))|J| = 2yです(J = 1 / 2 / sqrt(x - y)はヤコビアン)。
誤解の原因は,「誤解されても大丈夫なように,|J|が1になる変換(X = A + B,Y = A)を著者が選んだこと」です(素人読み)。
Mathematicaで確認します。
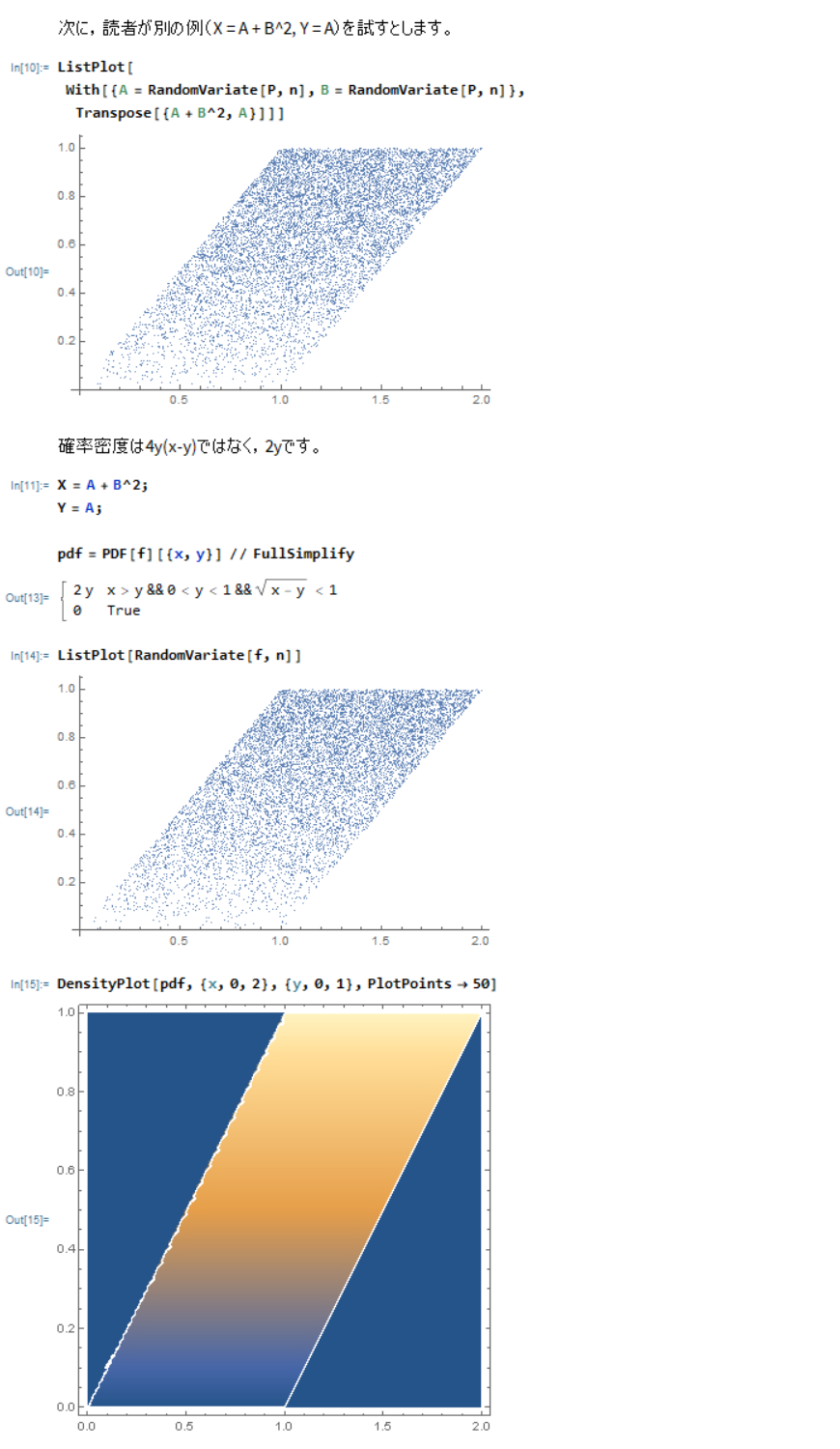
キャプチャ中のコードは以下の通りです。
ListPlot[
With[{A = RandomVariate[P, n], B = RandomVariate[P, n]},
Transpose[{A + B^2, A}]]]
X = A + B^2;
Y = A;
pdf = PDF[f][{x, y}] // FullSimplify
ListPlot[RandomVariate[f, n]]
DensityPlot[pdf, {x, 0, 2}, {y, 0, 1}, PlotPoints -> 50]
こういう具合に,指導対局の上手の工夫を探ろうと思うと,より一層楽しめる一冊です。
追記:「因果」って書いているところは全部「相関」に置き換えていいのではないかと思います。
