使っているのは整数の加算と乗算だけで、オーバーフローしているわけでもないのに正しく計算できない例を先日紹介しました（フェルマーの最終定理の「反例」（電卓編））。

文明が発達しすぎた果てに電卓を作れなくなってしまうというのはSFでよくありそうな話ですが、時代の先を行っているというAppleの主張は確かに正しいのかもしれません。（参考：ロストテクノロジー(Wikipedia)）

小数が出てくればいろいろ問題があるのは知っていても、電卓を使った整数の計算を疑う人は少ないのではないでしょうか。しかし実際には、WindowsやMac OS Xの標準的な電卓は、つい最近まで整数の計算を正しく行えませんでした。

1992年に発売されたWindows 3.1の電卓には、下のような普通の電卓と関数電卓の2種類のモードがありました（下はWindows 3.1の電卓を、Windows 7上、「プロパティ」で「互換モードWindows 95」を指定して実行した様子です）。

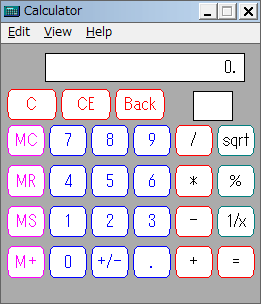
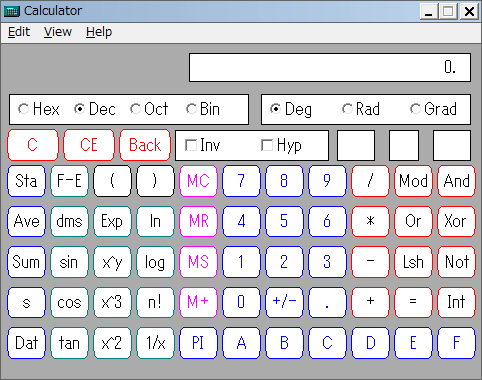
この、普通の電卓と関数電卓という構成は、2007年に発売されたWindows Vistaまで、基本的には変わりません（下はWindows Vistaの電卓。Windows 3.1のものと違って、Windows 7上では実行できないというのは皮肉なことです）。

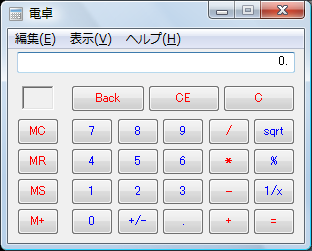
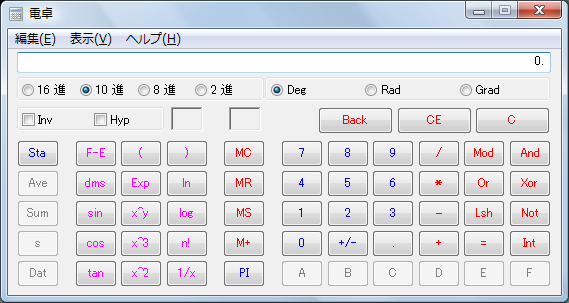
Windows 7では、電卓のUIが変更され機能も大幅に拡張されるということで、ちょっと話題になっていました。

Windows 95以来、スタートメニューのアクセサリには、電卓が含まれていた。その機能はVistaまでほとんど変わることなく続いてきた。（Windows 7ソフトウェアレビュー － 大きく進化した電卓編）

これは大間違いです。まあ、見た目がほとんど変わっていないので、そう思われるのもしかたがないのですが。私が試した限りでは、Windowsの電卓は、1995年に発売されたWindows 95と1999年に発売されたWindows 98SEの間では、その機能が大きく変わっています。計算の精度を高めることによって、フェルマーの最終定理の「反例」（電卓編）のような問題が起こらなくなったのです（参考：When you change the insides, nobody notices）。

一方Macはと言えば、1996年に発売されたMac OS 7.5.5の電卓は、下のような感じでした。1992年のWindows 3.1にかなり後れを取っている感じです。

Mac OS Xの電卓は、下のような基本・科学計算・プログラマの3つのモードを備えており、Windows Vistaのそれより優れているように見えます。

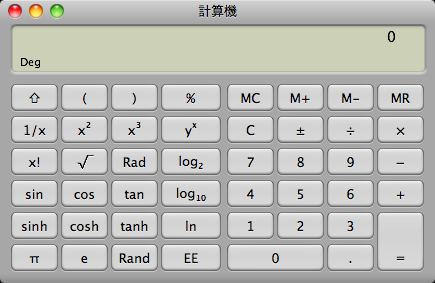
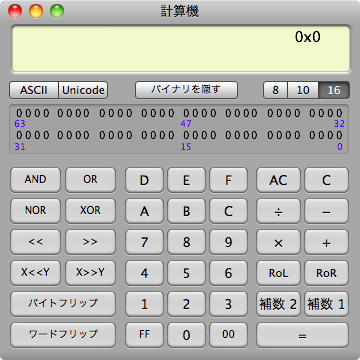
しかし、先に述べたようなMicrosoftが遅くとも1999年には修正できていた問題が、Macで修正されたのは2007年のMac OS X 10.5でのことでした（PowerPC版Mac OS X 10.4では、基本モードと科学計算モードで結果が異なり、しかも、両方とも間違っていました）。

同じくApple社のiPhoneの電卓はもっと大変で、Ver 2.0のバグはかなり大きく取り上げられましたし（参考：iPhone 2.0 の「計算機」アプリにバグが発見される）、本稿で扱っているような、大きな整数の計算を正しくできないという問題は、バージョンが3.1になった現在でも残っています。端末を回転させるとモードが切り替わるのもかっこよくていいのですが、その前にやるべきことがたくさんありそうです。

見た目をよくするのは大事なことです。しかし、電卓で最も大切なことは「正しく計算できること」であるということに疑問の余地はありません。

「正しく計算できること」を完璧に実現するのはもちろん不可能です。どのあたりで妥協するかが重要なわけですが、フリーソフトウェアのGNU bcの、「メモリが許す限りの桁数を確保する」というのは一つの目安になるでしょう。

やってはいけないのは、「整数はいわゆるintで計算し、その範囲を超えたり1未満の数が必要になったらいわゆるdoubleを使う」というような実装です。こういうことをしてしまうと、フェルマーの最終定理の「反例」（Perl, awk, JavaScript, PHP編）も発生してしまいます。

もっとも、電卓をちゃんと作るのは以外と難しいようで、2008年にはGoogleも計算ミスをしていました（参考：グーグルの電卓機能が計算ミス）。そのときには次のような解説がありましたが、その筆者が考える電卓の実装は、先に述べた「やってはいけないこと」そのままのようです。

コンピュータでの正確な計算は、コンピュータが一般的に0または1の数字しかない2進数で計算をしていることに基づいている。一方、人は0から9までの数字を使った10進数計算を行う。正確性に問題が生じるのは、コンピュータが数字を2進数に変換して処理し、結果を10進数に戻して表示するためだ。

このようなことが、電卓において問題になるはずはありません。

プログラミングの入門書などで、「電卓を作ってみよう！」なんていうのをたまに見かけますが、入門者に電卓はあまりいい題材ではありません（RubyやPythonなら問題ありません。他の言語でも、GMPを紹介するなら大賛成です）。

電卓を作るのもなかなか大変です。

メモ

電卓で整数の計算がある程度正確にできるようになった時期

  • Unix (GNU bc): 1994年（遅くとも）
  • Windows: 1999年（遅くとも）
  • Mac: 2007年

bcに関しては、もう少し歴史をさかのぼるべきかもしれません。bc (UNIX)

追記