ピタゴラス三体問題（Burrau’s problem of three bodies）

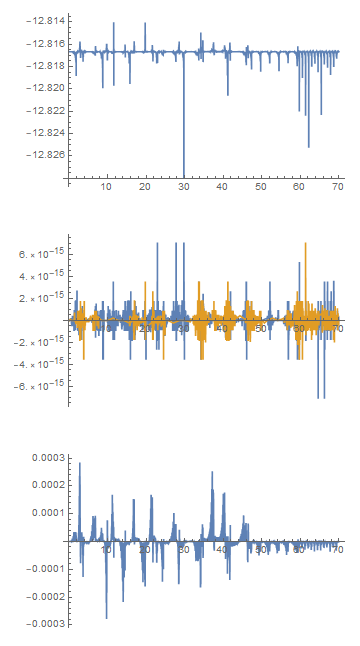
「三体問題」の有名なものに、ピタゴラス三体問題があります。図のような3:4:5の直角三角形の頂点上に静止させた、質量3, 4, 5の質点の運動を調べるというものです。追記：Mathematica 12で追加されたNBodySimulationを試す。

コンピュータサイエンスは重要だがコンピュータそのものが重要なわけではない、とミンスキー氏は強調した。それは解けない方程式があっても、コンピュータを使うことで何が起こるかを見る事ができるからだ。それがコンピュータがなく数学しかなかった時代との違いだとミンスキー氏はいわゆる「3体問題」など力学の問題を例に出して説明した。（機械で「心」を作る～「AIの父」ミンスキー氏が早稲田大学で講演）

この問題は1893年には知られていましたが、数値的にでさえ、解決は1966年になってからです。ディアク，ホームズ『天体力学のパイオニアたち』によれば、粒子の2つが連星を形成し、第3体が高速度ではじき飛ばされるという結論は、驚くべきものだったそうです。

これを数値的に解くのは、コンピュータ無しではまあ無理ですよね。「この問題をちゃんと解くのは大変ですよ」と言っていた天体力学の教授の言葉が思い出されますが、ちょうど、Mathematicaならケプラー問題の数値解を簡単に求められるという記事に対して、「でも、計算精度は大丈夫でしょうか」と訊かれたところだったので、コンピュータがあれば簡単だということを確認してみましょう。

必要な精度は状況によるので、絶対大丈夫とは言えませんが、たいていの場合には、十分よい精度で計算すると思います。有名なピタゴラス三体問題で調べてみましょう。

運動エネルギーとポテンシャルエネルギーから運動方程式を導き、数値的解きます。解く時は、保存量（全エネルギーと運動量、角運動量）が保存されるようにします。（コードは最後に掲載）

最初の70単位時間までの軌跡です．

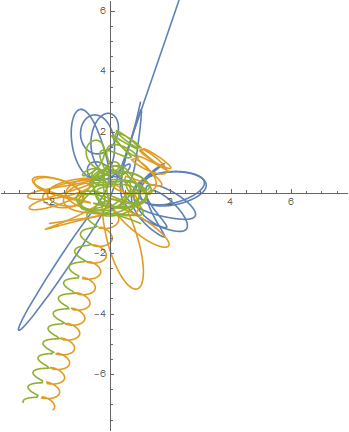
計算の正しさを証明するものではありませんが、この結果はBurrau’s problem of three bodiesで紹介されているものとだいたいあっています。（リンク先にはこの問題を数値的に解いたSzebehelyの論文があります。）

最初の70時間単位までのアニメーションです．

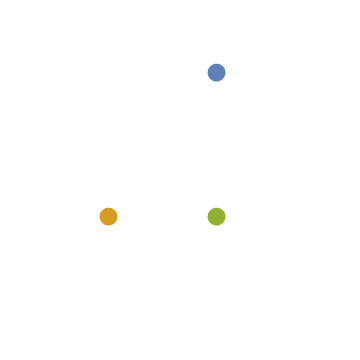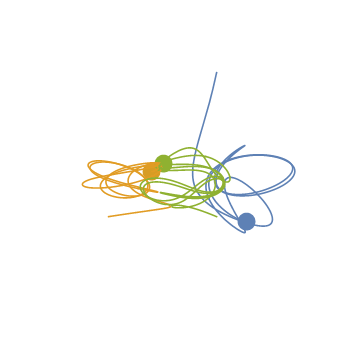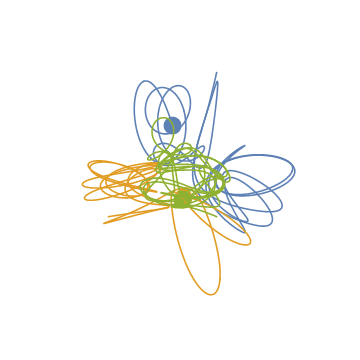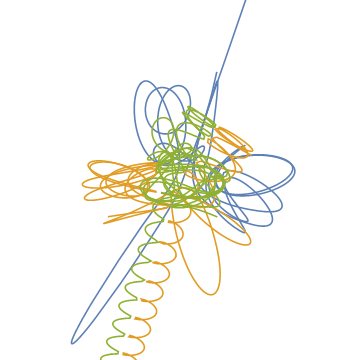
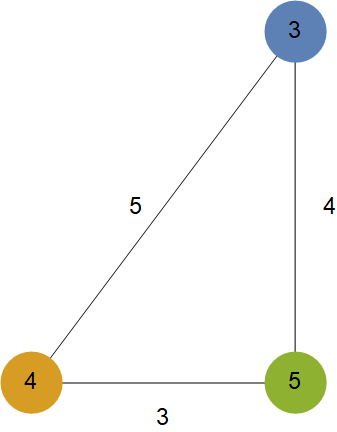
保存量が実際に保存されているかどうかを見ておきましょう。上から，エネルギー，運動量，角運動量です．